マクスウェルの方程式の帰結は、
である。φは電位、Ax、Ay、Azはベクトルポテンシャル、ρは荷電密度、
ix、iy、izは電流、ε0は真空の誘電率、μ0は
真空の透磁率である。cは光速である。
このうち(1)を解くことを考えよう。(1)が解ければ(2)、(3)、(4)も解ける。これは波動方程式と呼ばれる。
今、
を満たすGがあったとする(このGはグリーン関数と呼ばれる。)。 そうすると
は(1)の解である。
なぜなら(6)を(1)の左辺に代入すれば
となるからである。
従ってGを求めればφが求まる。(5)式から求める。
Gを
とフーリエ展開する。
(8)を(5)に代入すると
であるから
よって
を満たすグリーン関数gを求めれば(8)よりGが求まりφが求まる。
(11)の解gの一つは
である。 (12)を(8)に代入してみよう。Gは
(13)を(6)に代入して(1)の解、電位φを求めてみよう。
となる。
ρ(XYZ,t-r/c)は空間点(XYZ)における時刻t-r/cにおける荷電密度である。r/c秒前の(XYZ)における荷電密度を
表すことから(14)は遅延ポテンシャルと呼ばれる。光子がrを伝って到達する時間r/cだけ遅れるわけである。
ちなみに(11)の解の一つが(12)であることを証明しよう。
とフーリエ展開しよう。 (15)を(11)に代入すれば
だから
これを(15)に代入すれば
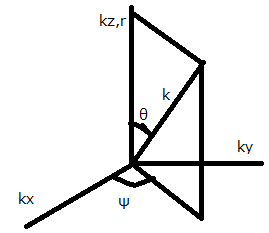
kx-ky-kz直交座標を用い、r=(x-X,y-Y,z-Z)を
kz軸と一致させると、極座標(k,θ,ψ)で、
kx(x-X)+ky(y-Y)+kz(z-Z)
は内積krcosθに等しい。また体積要素dkxdkydkz=dVは
dV=k2sinθdkdθdψ
となるから
よって
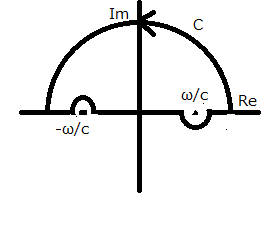
閉曲線Cに極-ω/cを含めずω/cを含めると、
(コーシーの積分定理)
(コーシーの積分公式)
よって解(12)が得られた。
参考文献
1)朝倉現代物理学講座「素粒子」原康夫 朝倉書店 1984年
2)新物理学シリーズ12「電気力学」平川浩正 培風館 昭和56年
3)速修「物理数学の応用技法」大谷俊介 プレアデス出版 2012年
メモ